去年七八月份的一个契机使我开始审视自己对密码学的理解,随后也陆续着手把这些知识的复习提上日程。说老实话,以目前赶项目的进度挤时间学习真是很困难。直到年末接连开始量产爬坡才抽身出来收集资料,想着趁今年春节不回家过年可以先把AES过掉,结果放假前一天下午实在没忍住买了麦田四号J的模型,也在这里顺便预告模型制作的文章好了。按照正常的假期来算,这篇文章势必要拖更,但是赶上春节爆发的流感疫情,返工时间推迟。世事难料,或许这段日子在未来会被称作为一个特殊的节点。既然说到这里,干脆多说两句,希望日后自己回看时能够想起一些事情。
Be a good man, do the right thing.
保留住美好的品质,与各位共勉
I. 概述
Advanced Encryption Standard,在密码学中表示高级加密标准,采用了比利时密码学家Joan Daeman与Vincent Rijmen所设计的Rijdael算法,严格来说,AES与Rijdael并不能划等号。AES被用于替代逐渐无法满足安全性能要求的DES(Data Encryption Standard)算法。同为对称加密,AES采用了置换-组合的结构,与DES所用的feistel结构是完全不同的。
文章将以FIPS-197文档为基础理论支撑,第五版密码编码学与网络安全教材作为辅助补充,代码大部分参考matt_wu的开源项目。本文描述的最终实现代码可以在这里获取。
II. 预备知识
以教材为例,在进入AES之前会有一个章节专门讲解数论与有限域的基本概念。AES的实现过程中,S盒,轮密钥生成,列混淆等操作都依赖GF(28)中多项式计算。掌握有限域概念及相关多项式模运算过程,才能够理解代码中实现的计算方式与流程。
FIPS-197有一份非常好的中文翻译版本,有疑惑时可以作为对照参考。此外,第2章定义中的两个小节也是值得认真一看,后文内容与代码实现都基于这些基本定义的描述。
位操作
提及位操作算是用现在的眼光对当时的学习经历做一个复盘,就我自己而言,进入到密码学课程时,仍然对很多基础概念的实操不够,没能很好地呼应理论中覆盖的一些知识点。有时甚至觉得我们专业里把int当成最小数据单元的人都不在少数,相比之下,嵌入式方向的同学们对这一块就要熟悉的多了。
正如简介中所说,Rijndael用128,192或256 比特长度密钥处理128比特的数据块。所以各个转换过程中少不了位操作参与。
与之相关主要提两个地方,一是位运算符,对左移右移位与位或之类的操作至少不要不知所云。二是注意传入参数的数据类型长度,从内存中取值时在这里犯错就非常恶心。例如后文会提到的,对等效逆变换过程中改写轮密钥生成函数时,需要注意一处数据类型转换。
Rijndael Animation
这个超经典的AES加密过程动画,接下来要讨论的问题全部都在这个动画中有展示。为了方便比对每一轮中发生的变化是否正确,代码中测试输入也是来自于这里。
state
state,就是上小节动画中出现的4行4列小方块,在中文语境中常被译为“体”或“状态矩阵”,如魔方的一个面一般,是轮函数处理数据的一种抽象结构。
从下图中下标序号也可以看出,数据是以“列”的方式依次排列在4x4矩阵中。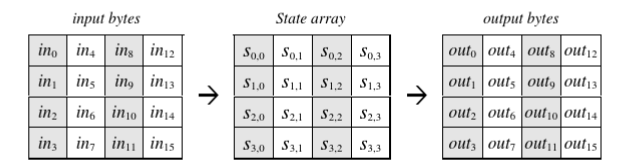
III. Math is the power
GF(2n),多项式,二进制以及字节
与数学有关的讨论最初往往令人望而却步,但深入后又是极有意思的。
AES涉及到的计算都落在有限域GF(28)中。有限域的概念在这里就不展开,课本的第4章有详细描述。作为复习,主要说说以下两点:为什么需要阶为素数,即模素数运算?为什么AES要取28?
- 首先模算术运算可以确保计算结果落在限定的范围内,即mod p后结果集合的取值区间为[0, p-1],是有限的。而p取素数则能够保证集合中所有元素都存在加法逆元与乘法逆元,即组成一个域。加法逆元容易满足,乘法逆元令p为一个合数即可反证。
- 28的特殊之处在于8个bit位组成了一个字节。用8个二进制位能够表示0到255之间的256个整数。但256不是素数,模256的运算结果无法组成一个域。小于256中的最大素数是251,但是使用251处理数据就浪费了251到255的数值表示,聪明节俭的工程师们是绝对不允许浪费存储空间这种伤天害理的事情发生。那么转机就是GF(28)。当然,单纯的模28与模256没有区别,依旧无法构成域,因此不能使用整数的模算术,需要通过多项式算术来构造所需的域,以多项式的系数对应比特值。
为了使系数对应二进制比特位,区别于一般的计算方法,需要使系数落在GF(2)上,即执行模2算术,所以系数取值只能为0或1;合并同类项时,系数进行异或操作,而非加法操作;加法与减法计算是相同的。如:
(x7+x5+x2+x) + (x5+x4+x2+1) = x7+x4+x+1
当然,这里的加号实际指⊕。
而处理四字节字(word)的时候,多项式系数又代表了域内的字节值,加法执行字节间的异或操作。乘法则根据降次的需求选取特定的模多项式,进行模运算。
那么本章各小节将对涉及到的基本数学概念与计算做相关描述。
加法
本节的加法特指二元加法运算,即模2加法运算,最终等价于对应比特位的异或操作。
(0+0) mod 2 = 0 ⟹ 0⊕0 = 0
(0+1) mod 2 = 1 ⟹ 0⊕1 = 1
(1+0) mod 2 = 1 ⟹ 1⊕0 = 1
(1+1) mod 2 = 0 ⟹ 1⊕1 = 0
且可证减法与加法结果完全相同。
由于这样的特殊性质,加法不需要单独编写一个函数,直接用异或操作符即可简单实现。
在多项式中,加法有如下表达:
(x6+x4+x2+x+1) + (x7+x+1) = x7+x6+x4+x2
以二进制表示为 { 01010111 } ⊕ { 10000011 } = { 11010100 }
十六进制表示为 {57} ⊕ {83} = {d4}
乘法
GF(28)上的乘法运算,实质上是多项式的乘积模次数为8的不可约多项式运算。所以在说明该运算时,会反复使用到 m(x) = x8+x4+x3+x+1,这是由作者钦定的多项式。同样,容易理解域内含有256个小于8次的多项式,这些多项式恰好对应了0-255这256个整数。此外,还会经常看到0x1b这个十六进制数的出现。它们之间的联系是一种计算技巧,基于这样一个等式:
在GF(2n)中,对于n次多项式p(x),有 xn mod p(x) = p(x) - xn
带入n = 8,有 x8 mod m(x) = m(x) - x8 = x4+x3+x+1
在之前的章节中提到过,多项式形式表达是将二进制比特位的值对应到多项式的系数,那么m(x)对应的二进制数为(0000 0001 0001 1011),表达为0x11b。m(x)是一个8次多项式,注意转化后是0x11b。如何得到0x1b,就需要再做下面的推导。现在将单项式xn扩展为多项式p(x)。
存在GF(28)中的多项式p(x) = a7x7+a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0
因多项式p(x)已处于域内无需额外运算,令p'(x) = p(x)$\cdot$x,有:
p'(x) = a7x8+a6x7+a5x6+a4x5+a3x4+a2x3+a1x2+a0x
注意此时系数在GF(2)上,其取值只有0与1。
当a7为0时,p'(x)次数为7,同样无需额外运算,直接得到结果为:
a6x7+a5x6+a4x5+a3x4+a2x3+a1x2+a0x
当a7为1时,根据之前引用的既约多项式与n次模算术运算,有:
p'(x) mod m(x) = (a6x7+a5x6+a4x5+a3x4+a2x3+a1x2+a0x) + (x4+x3+x+1)
将多项式系数对应到二进制比特位,则有:
那么当a7 = 1时,式中的(0001 1011)即为0x1b。这个值是给定的既约多项式在有限域GF(28)中计算的必然结果。以上就是代码中0x1b的来源。
为了加深印象,先用最淳la朴ji的方法计算{a6}与{59}在GF(28)中的乘法结果,再通过下一小节熟悉如何使用0x1b取得相同的结果。
首先将hex转化为多项式,{a6}为(1010 0110),对应x7+x5+x2+x
{59}则为(0101 1001),对应x6+x4+x3+1
(x7+x5+x2+x)$\cdot$(x6+x4+x3+1)
= x13+x11+x11+x10+x9+x8+x8+x7+x7+x6+x5+x5+x5+x4+x2+x
= x13+x11+x11+x10+x9+x8+x8+x7+x7+x6+x5+x5+x5+x4+x2+x
= x13+x10+x9+x6+x5+x4+x2+x
in GF(28),将乘积做模运算,过程如下图
可以算出 {a6}$\cdot${59} = {61}
代码中肯定不能以这种试商法来实现,所以引出了下一节,乘X。
乘X
抓住本质,乘法就是多个相同数字求和的简便运算。而口诀表,是人们创造出来以节约时间的查表法,牺牲存储空间换取速度。通过乘X的方法,多项式任意指数都可以通过递归调用公式1获得。
概括为以下两点:
- 00 - FF 中所有的数都可以通过以下八个数的组合位运算得到
1000 0000 ⟹ 0x80
0100 0000 ⟹ 0x40
0010 0000 ⟹ 0x20
0001 0000 ⟹ 0x10
0000 1000 ⟹ 0x08
0000 0100 ⟹ 0x04
0000 0010 ⟹ 0x02
0000 0001 ⟹ 0x01
- 乘法是加法的组合,在GF(28)将加法与乘法对应表达为⊕与$\cdot$
仍然计算{a6}$\cdot${59},过程如下:
$\because$ {59} 由 {40}⊕{10}⊕{08}⊕{01} 构成
$\therefore$ {a6}$\cdot${59} = {a6}$\cdot$({40}⊕{10}⊕{08}⊕{01})
计算所有中间值
{a6}$\cdot${01} = {a6}
{a6}$\cdot${02} = xtime({a6}) = {57}
{a6}$\cdot${04} = xtime({57}) = {ae}
{a6}$\cdot${08} = xtime({ae}) = {47}
{a6}$\cdot${10} = xtime({47}) = {8e}
{a6}$\cdot${20} = xtime({8e}) = {07}
{a6}$\cdot${40} = xtime({07}) = {0e}
{a6}$\cdot${80} = xtime({0e}) = {1c}
带入右式展开
{a6}$\cdot${59}
= ({a6}$\cdot${40})⊕({a6}$\cdot${10})⊕({a6}$\cdot${08})⊕({a6}$\cdot${01})
= {a6}⊕{47}⊕{8e}⊕{0e}
= {61}
在C中,使用移位与异或运算可以很容易地实现。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32//多项式在GF256中的运算
uint8_t GF256_xtime(uint8_t x)
{
return ((x << 1) ^ (((x >> 7) & 1) * 0x1b));
}
//AES定义的乘X运算
//参数ts代表移多少次位,取值为0-7
uint8_t aes_xtimes(uint8_t x, int ts)
{
while (ts-- > 0)
{
x = GF256_xtime(x);
}
return x;
}
//GF(2^8)中的多项式乘法运算
//参数x做“乘X”运算,获取所有中间值
//再与多项式y中系数为1的项做异或
uint8_t aes_mul(uint8_t x, uint8_t y)
{
return ((((y >> 0) & 0x01) * aes_xtimes(x, 0)) ^
(((y >> 1) & 0x01) * aes_xtimes(x, 1)) ^
(((y >> 2) & 0x01) * aes_xtimes(x, 2)) ^
(((y >> 3) & 0x01) * aes_xtimes(x, 3)) ^
(((y >> 4) & 0x01) * aes_xtimes(x, 4)) ^
(((y >> 5) & 0x01) * aes_xtimes(x, 5)) ^
(((y >> 6) & 0x01) * aes_xtimes(x, 6)) ^
(((y >> 7) & 0x01) * aes_xtimes(x, 7)) );
}
系数在GF(28)中的多项式
这一节的标题是"Polynomials with Coefficients in GF(28)",是MixColumns变换的理论基础。需要思考两点:为什么要强调系数的范围?它与之前章节的计算有什么不同?
前文中讨论GF(28)计算,将对应项的系数与二进制比特位值划上等号有一个重要的前提条件,那就是多项式的系数做了模2运算。但是算法中有时会将四字节的向量考虑为多项式,即系数在有限域中的四项式,表达如下:
a(x) = a3x3+a2x2+a1x+a0
本节中描述的系数本身就是有限域GF(28)中的元素,所以系数是字节byte。而之前章节中用多项式表示字节,系数是比特位的值bit,这点需要注意区分。
多项式的含义发生了变化,所以需要定义新的加法与乘法运算规则。
有限域中的加法仍然是异或运算,只不过将其扩展为字节间的异或。定义另一个多项式b(x),有:
b(x) = b3x3+b2x2+b1x+b0
加法运算为:
c(x) = a(x)+b(x)
= (a3⊕b3)x3+(a2⊕b2)x2+(a1⊕b1)x+(a0⊕a0)
乘法则相对复杂,因为现在的系数在GF(28)而不在GF(2)了,需要分为两步。
首先将系数全部计算:
c(x) = a(x)$\cdot$b(x) 是一个六次多项式:
= c6x6+c5x5+c4x4+c3x3+c2x2+c1x+c0
且易得各系数分别为:
c0 = a0$\cdot$b0
c1 = a1$\cdot$b0⊕a0$\cdot$b1
c2 = a2$\cdot$b0⊕a1$\cdot$b1⊕a0$\cdot$b2
c3 = a3$\cdot$b0⊕a2$\cdot$b1⊕a1$\cdot$b2⊕a0$\cdot$b3
c4 = a3$\cdot$b1⊕a2$\cdot$b2⊕a1$\cdot$b3
c5 = a3$\cdot$b2⊕a2$\cdot$b3
c6 = a3$\cdot$b3
不加处理的情况下,六次多项式无法表示四字节向量,所以第二步就是通过模运算降次。
在AES中,选择了x4+1作为模多项式。a(x)⊗b(x)的完整计算过程如下:
定义四项式d(x) = d3x3+d2x2+d1x+d0
根据计算结果,有:
d0 = (a0$\cdot$b0)⊕(a3$\cdot$b1)⊕(a2$\cdot$b2)⊕(a1$\cdot$b3)
d1 = (a1$\cdot$b0)⊕(a0$\cdot$b1)⊕(a3$\cdot$b2)⊕(a2$\cdot$b3)
d2 = (a2$\cdot$b0)⊕(a1$\cdot$b1)⊕(a0$\cdot$b2)⊕(a3$\cdot$b3)
d3 = (a3$\cdot$b0)⊕(a2$\cdot$b1)⊕(a1$\cdot$b2)⊕(a0$\cdot$b3)
以矩阵方式表达为:
IV. AES
我们可以找到很多AES总体结构的说明图片,为了让这篇文章显得长一点,也放一张吧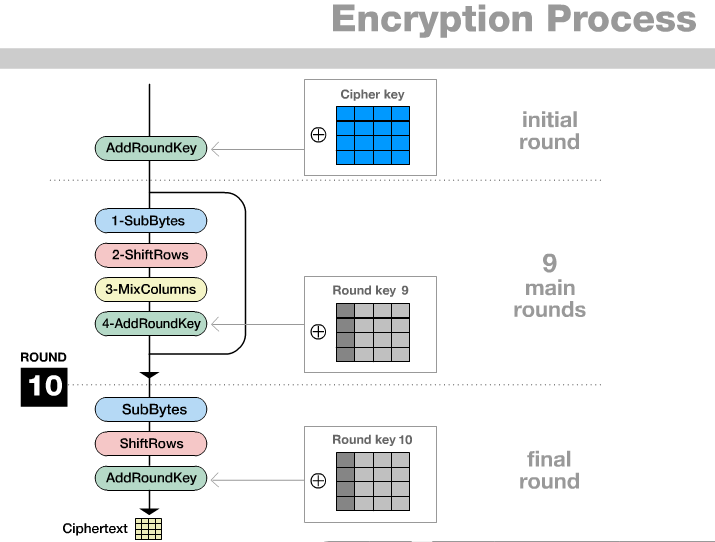
我一直在想,当然这个想法应该是看油管印度街头小吃视频启发的,AES有点像三哥们煮的糊糊,一边处理食材另一边处理酱料,处理好之后倒在一起一通乱搅,然后接着处理2号食材处理2号酱料再一搅,如此循环个10轮就是AES-128了,反正最后端出来没人知道究竟是什么做的。相比之下DES像麻花,左右两段扭在一起炸至金黄酥脆。扯远了扯远了 (*ˉ﹃ˉ) 。
在理解AES的时候,可以把上面的结构说明拆成两大部分,分别为加解密过程与密钥策略。在FIPS-197的第五章中,是以5.1加密,5.2密钥扩展,5.3解密的顺序描述。在这里先聊前两个过程。
PART A 加密过程
这个部分就是FIPS-197 5.1 Cipher小节,请出教材神图,表示了AES一轮加密的过程,反正我第一次看的时候真是WTF的状态。解释一下,把state的4x4形式以一维展开,从左到右为字节0到字节15。把shiftrows画成矩阵的样子做对比,这样就比较好理解了。并且图片的展开方式,比较类似于线性存储在内存中数据的变化过程,抽象数据结构的时候也可以参考此图。
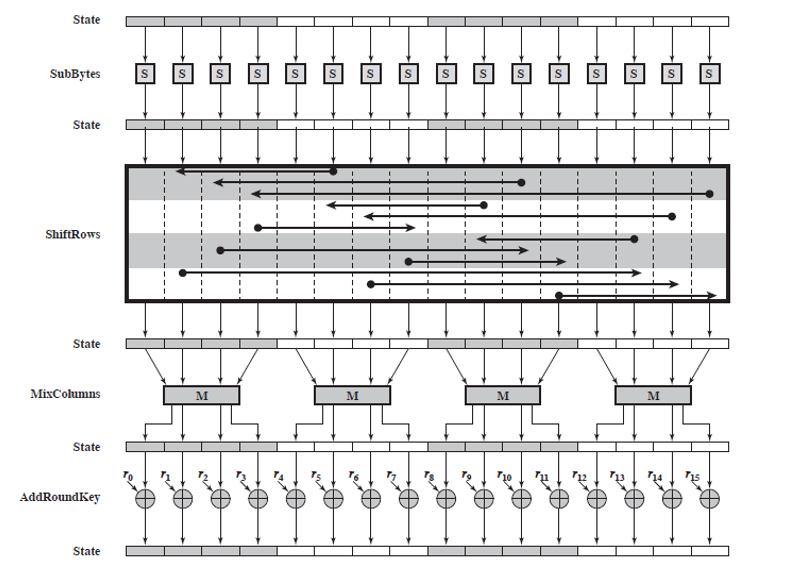
SubBytes
SubBytes被译为字节替代,替代的来源就是老师反复会提及的S盒。关于用S盒,参考文献中贴了一篇看雪的帖子,个人认为非常值得一读。
SubBytes在整个算法中充当非线性变换作用,说枯燥一点,它做了GF(28)中的乘法逆运算与GF(2)中的仿射变换。另外要说明的是,达到要求的安全性,考虑输入输出的相关性,满足可逆等等,选择一个足够好的S盒并不容易。S盒绝对值得用大篇幅来讨论,我想在这里做的功利一点,先不讨论S盒的原理,直接查表可得。
那么这个16行16列的盒子为域内所有的256个元素都准备了一套新马甲:
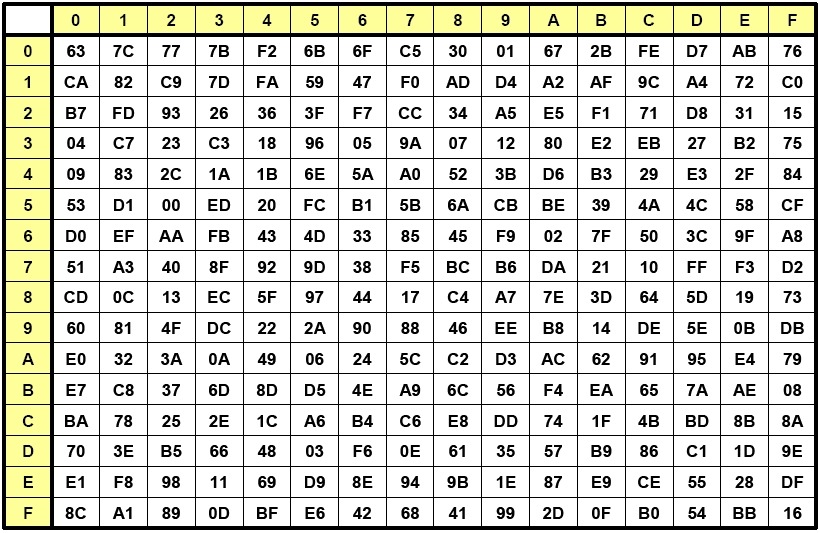
代码实现1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43//硬编码S盒
/* aes sbox and invert-sbox */
static const uint8_t g_aes_sbox[256] = {
/* 0 1 2 3 4 5 6 7 8 9 A B C D E F */
0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76,
0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0,
0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15,
0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75,
0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84,
0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf,
0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8,
0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2,
0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73,
0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb,
0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08,
0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a,
0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e,
0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf,
0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16
};
//封装调用方法
uint8_t sbox(uint8_t val)
{
return g_aes_sbox[val];
}
//5.1.1 SubBytes
//使用S盒替换原始数据
void aes_sub_bytes(AES_CYPHER_T mode, uint8_t *state)
{
int i, j;
//4行4列的state
for (i = 0; i < 4; i++)
{
for (j = 0; j < 4; j++)
{
//把值给S盒的下标取出新值
state[i * 4 + j] = sbox(state[i * 4 + j]);
}
}
}
ShiftRows
ShiftRows,即行移位。可以说是相对容易理解的一个环节,state的最后三行分别做一二三位的循环左移,矩阵表达已在前文中列出。
行移位变换能够将某个字节从一列转移到另一列中,事实上是将原本state的一列扩散到了不同的四列中。实现简洁,但结合state以列做为运算基础,与其他轮函数配合能够达到足够可观的扩散效果。
直接来看代码实现:
1 | //cyclically shifted over the given number |
MixColumns
MixColumns列混淆,我认为是PartA中综合难度最高的一个变换。起码抛开原理,查表法的S盒替换对于纯粹代码编写毫无难度(当然使用生成元方式还是需要花功夫研究的),但列混淆的实现我着实想了很久。甚至到今天,对于编码线性变换的混淆程度也没有很深入地去研究。综合一些搜集到的资料和相关问题的讨论,我比较倾向于这样一个观点:列混淆变换在算法安全要求与计算复杂度间做到了很取巧的平衡。其多项式容易计算,逆运算也不算太复杂,又能够在列中达到足够的混淆效果。当然相比之下逆运算会更困难,不过AES中加密被认为比解密更加重要->课本P116,可以说是无伤大雅。
MixColumns变换将state的每一列都看作GF(28)中的多项式,与给定多项式a(x)相乘后,做模x4+1运算,得到的余式即最终结果。其中给定的a(x)为
在3.5小节中详细演算过通用多项式的计算过程,在这里将a(x)系数带入(2)式的结论,可得s'(x) = a(x) ⊗ s(x)的计算如下:
S'0,c = ({02} $\cdot$ S0,c) ⊕ ({03} $\cdot$ S1,c) ⊕ S2,c ⊕ S3,c
S'1,c = S0,c ⊕ ({02} $\cdot$ S1,c) ⊕ ({03} $\cdot$ S2,c) ⊕ S3,c
S'2,c = S0,c ⊕ S1,c ⊕ ({02} $\cdot$ S2,c) ⊕ ({03} $\cdot$ S3,c)
S'3,c = ({03} $\cdot$ S0,s) ⊕ S1,c ⊕ S2,c ⊕ ({02} $\cdot$ S3,c)
矩阵表达为:
所以在这一节需要完成矩阵C到矩阵A的转化。将state每列中对应字节做GF(28)乘法并异或,实现代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37//5.1.3 mix columns
//each column considered as a polynomials multiplied with
//a fixed polynomial a(x) then modulo x^4+1 over GF(2^8)
//note the given a(x) = {03}x^3 + {01}x^2 + {01}x^1 + {02}x^0
void aes_mix_columns(AES_CYPHER_T mode, uint8_t *state)
{
//常数矩阵的一维表示
uint8_t y[16] = { 2, 3, 1, 1, 1, 2, 3, 1, 1, 1, 2, 3, 3, 1, 1, 2};
uint8_t s[4];
//i-column index of state, max is 4
//j-multiply index, max is 4
//r-row index of a(x) replaced martix, max is 4
int i, j, r;
//state multiplicate fixed a(x)
for (i = 0; i < g_aes_nb[mode]; i++)
{
//each column of state and a(x)
for (r = 0; r < 4; r++)
{
s[r] = 0;
//column multiply a(x)
for (j = 0; j < 4; j++)
{
//调用aes乘法得到变换后的字节值,即3.4小节 乘X
s[r] = s[r] ^ aes_mul(state[i * 4 + j], y[r * 4 + j]);
// printf("%02x ", s[r]);
}
}
// printf("\r\n");
//传入新的state中
for (r = 0; r < 4; r++)
{
state[i * 4 + r] = s[r];
}
}
}
其实可以看到,第二节中封装的aes_mul只会在mixcolumns与其逆运算中使用到。且实际在AES中,aes_mul对应的计算需求并没有覆盖整个有限域,与选定的模多项式有关,最终仅对0,1,2,3,9,b,d,e这几个值运算。
AddRoundKey
轮密钥加作为PART A中的变换来看是非常简单的,计算轮密钥的过程放在下一个小节中探讨,在已有轮密钥的前提下,128位的state按位与128位的轮密钥做异或,或者看作16个字节间的异或。异或运算不需要构造逆运算,其操作就是自身的逆。代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13//5.1.4 add round key
void aes_add_round_key(AES_CYPHER_T mode, uint8_t *state, uint8_t *round, int nr)
{
//把地址丢进去,算完取值即可
uint32_t *w = (uint32_t *)round;
uint32_t *s = (uint32_t *)state;
int i;
for (i = 0; i < g_aes_nb[mode]; i++)
{
s[i] ^= w[nr * g_aes_nb[mode] + i];
}
}
最终,完整的加密过程实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51int aes_encrypt(AES_CYPHER_T mode, uint8_t *data, uint8_t *key)
{
uint8_t w[4 * 4 * 15] = {0}; /* round key */
uint8_t s[4 * 4] = {0}; /* state */
int nr;
/* key expansion */
aes_key_expansion(mode, key, w);
/* init state from user buffer (plaintext) */
memcpy(s, data, 4 * g_aes_nb[mode]);
/* start AES cypher loop over all AES rounds */
for (nr = 0; nr <= g_aes_rounds[mode]; nr++)
{
printf(" [Round %d]\n", nr);
aes_dump("input", s, 4 * g_aes_nb[mode]);
if (nr > 0)
{
/* do SubBytes */
aes_sub_bytes(mode, s);
aes_dump("SubBytes", s, 4 * g_aes_nb[mode]);
/* do ShiftRows */
aes_shift_rows(mode, s);
aes_dump("ShiftRows", s, 4 * g_aes_nb[mode]);
if (nr < g_aes_rounds[mode])
{
/* do MixColumns */
aes_mix_columns(mode, s);
aes_dump("MixColumns", s, 4 * g_aes_nb[mode]);
}
}
/* do AddRoundKey */
aes_add_round_key(mode, s, w, nr);
aes_dump("RoundKey", &w[nr * 4 * g_aes_nb[mode]], 4 * g_aes_nb[mode]);
aes_dump("state", s, 4 * g_aes_nb[mode]);
}
/* save state (cypher) to user buffer */
memcpy(data, s, 4 * g_aes_nb[mode]);
printf("Output:\n");
aes_dump("cypher", data, 4 * g_aes_nb[mode]);
return 0;
}
其中的aes_dump是我实现的state内容打印函数,aes_key_expansion在下一节密钥策略中描述。
PART B 密钥策略
密钥扩展主要用来防止已有的密码分析攻击,将16字节的初始密钥根据Nk扩展出相应的轮密钥。过程有些繁杂,可以结合rijndaelanimation动画学习。也有很多论文对AES提出的密钥策略做了相关的增强,有兴趣可以扩展一下,这里还是基于FIPS-197对AES-128的情况进行描述。
KeyExpansion
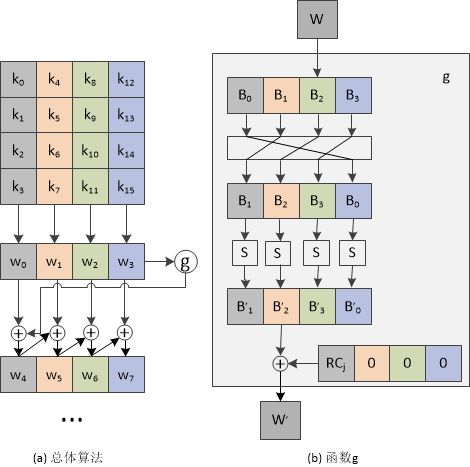
密钥扩展过程包含SubWord,RotWord和列异或几个过程。其中SubWord将输入的列用S盒做置换,RotWord将列中第一个元素移到列末尾,列异或则是将一个state中的列与上一个state相同位置的列做异或运算。密钥扩展中有一个需要注意的Rcon,在第二章中介绍Rcon指The round constant word array,即轮常量字数组。我在实现的时候老是把这个Rcon联想成Recon,果然是叛乱里经常随机到侦察兵做领队,已经走火入魔了吗┗|`O′|┛
Rcon的代码实现1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18/*
* aes Rcon:
* round constant for key expansion
* WARNING: Rcon is designed starting from 1 to 15, not 0 to 14.
* FIPS-197 Page 9: "note that i starts at 1, not 0"
*
* i | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
* -----+------------------------------------------------------------------------------------------
* | [01] [02] [04] [08] [10] [20] [40] [80] [1b] [36] [6c] [d8] [ab] [4d] [9a]
* RCON | [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00]
* | [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00]
* | [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00] [00]
*/
static const uint32_t g_aes_rcon[] = {
0x01000000, 0x02000000, 0x04000000, 0x08000000, 0x10000000, 0x20000000, 0x40000000, 0x80000000,
0x1b000000, 0x36000000, 0x6c000000, 0xd8000000, 0xab000000, 0xed000000, 0x9a000000
};
同样,SubWord和RotWord也容易实现1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26//function used in the Key Expansion routine that takes a four-byte input word
//and applies an sbox to each of the four bytes to produce an output word.
//32bits double word which is the four-byte input
uint32_t aes_sub_dword(uint32_t val)
{
//用tmp接收结果
uint32_t tmp = 0;
//aes_sub_sbox的参数为uint8_t类型
//传入4字节数据,通过强转分别获取每个字节的置换结果,最后或入tmp中
tmp |= ((uint32_t)aes_sub_sbox((uint8_t)((val >> 0) & 0xFF))) << 0;
tmp |= ((uint32_t)aes_sub_sbox((uint8_t)((val >> 8) & 0xFF))) << 8;
tmp |= ((uint32_t)aes_sub_sbox((uint8_t)((val >> 16) & 0xFF))) << 16;
tmp |= ((uint32_t)aes_sub_sbox((uint8_t)((val >> 24) & 0xFF))) << 24;
return tmp;
}
//function used in the Key Expansion routine that takes a four-byte word and
//performs a cyclic permutation
//32bits double word as input
uint32_t aes_rot_dword(uint32_t val)
{
uint32_t tmp = val;
//循环移位
return (val >> 8) | ((tmp & 0xFF) << 24);
}
密钥扩展的实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45//key expansion, get round key
void aes_key_expansion(AES_CYPHER_T mode, uint8_t *key, uint8_t *round)
{
uint32_t *w = (uint32_t *)round;
uint32_t t;
int i = 0;
printf("Key Expansion:\n");
do {
w[i] = *((uint32_t *)&key[i * 4 + 0]);
//输出初始的state四列内容
printf(" %2.2d: rst: %8.8x\n", i, aes_swap_dword(w[i]));
} while (++i < g_aes_nk[mode]);
do {
printf(" %2.2d: ", i);
if ((i % g_aes_nk[mode]) == 0)
{
//每个轮密钥state的第一列要进行subword,rotword和异或rcon
t = aes_rot_dword(w[i - 1]);
printf(" rot: %8.8x", aes_swap_dword(t));
t = aes_sub_dword(t);
printf(" sub: %8.8x", aes_swap_dword(t));
printf(" rcon: %8.8x", g_aes_rcon[i / g_aes_nk[mode] - 1]);
t = t ^ aes_swap_dword(g_aes_rcon[i / g_aes_nk[mode] - 1]);
printf(" xor: %8.8x", t);
}
else if (g_aes_nk[mode] > 6 && (i % g_aes_nk[mode]) == 4)
{
//AES-256的特殊处理
t = aes_sub_dword(w[i - 1]);
printf(" sub: %8.8x", aes_swap_dword(t));
}
else
{
//除去第一列外,剩下的三列无需处理,等待与上一个state中对应列做异或
t = w[i - 1];
printf(" equ: %8.8x", aes_swap_dword(t));
}
w[i] = w[i - g_aes_nk[mode]] ^ t;
printf(" rst: %8.8x\n", aes_swap_dword(w[i]));
} while (++i < g_aes_nb[mode] * (g_aes_rounds[mode] + 1));
/* key can be discarded (or zeroed) from memory */
}
以AES-128为例,输入的4个字(16字节)将被扩展为44个字(176字节)的一维线性数组。如果将加密过程看作主菜,那么密钥扩展就像是酱料的调配,是一个相对独立的过程。事实上我在实现AES时也正是这样做的,在github的commit中可以看到,第一阶段先完成了所有的轮密钥生成。
轮密钥log详见附录A。
解密过程
不同于使用Feistel结构的DES,AES中的解密需要实现加密的逆变换。
这一节在FIPS-197中的描述比较简单,而教材是以轮函数为视角,在各小节中统一介绍正向与逆向变换。总之,InvShiftRows是循环右移1、2、3字节,InvSubBytes找逆S盒,InvMixColumns用a(x)的乘法逆元,AddRoundKey做异或所以逆为自身。实现时参考FIPS-197第21页图12的伪代码,解密过程的轮函数调用顺序为:
InvShiftRows->InvSubBytes->AddRoundKey->InvMixColumns
这是很有趣的一个地方,可以与15页图5加密过程的伪代码对比体会。在本文的第六章节还会深入讨论逆运算的等价过程。这里先贴上根据图12实现的解密部分代码:
1 | int aes_decrypt(AES_CYPHER_T mode, uint8_t *data, uint8_t *key) |
V. 输出实例
这一章单独贴加解密打印,包含了每一轮的输入、变换后结果与输出,可以和rijndaelanimation对比验证。
内容详见附录B
VI. 还有一些问题
1. 轮函数调用的探讨
在matt_wu给出的源码中,解密部分即Inverse Cipher,函数实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18/* start AES cypher loop over all AES rounds */
for (nr = g_aes_rounds[mode]; nr >= 0; nr--) {
/* do AddRoundKey */
aes_add_round_key(mode, s, w, nr);
if (nr > 0) {
if (nr < g_aes_rounds[mode]) {
/* do MixColumns */
inv_mix_columns(mode, s);
}
/* do ShiftRows */
inv_shift_rows(mode, s);
/* do SubBytes */
inv_sub_bytes(mode, s);
}
}
实际上其轮函数的调用过程为,先做了一轮 AddRoundKey, invShiftRows, invSubBytes,再按照 addRoundKey, invMixColumns, invshiftRows, invSubBytes 的顺序做剩下的 nr-1 轮,最后做一个AddRoundKey。
起初我也没有察觉到有什么异样,在验证的过程中发现加解密每轮的输出不能相互印证,仔细一看觉得这里有点怪。
我按照文档实现的代码为:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15for (nr = g_aes_rounds[mode]; nr >= 0; nr--)
{
if (nr < g_aes_rounds[mode])
{
inv_shift_rows(mode, s);
inv_sub_bytes(mode, s);
}
aes_add_round_key(mode, s, w, nr);
if (nr < g_aes_rounds[mode] && nr > 0)
{
inv_mix_columns(mode, s);
}
}
//加解密的轮是否需要相呼应?
~~是否需要满足加解密过程中,相应的轮函数执行完毕,此时内存中的state恰好可以互为输入输出?
如上节log中解密第八轮做invMixColumns输出的state为:
invMixColumns:
49 45 7f 77
db 39 02 de
87 53 d2 96
3b 89 f1 1a
应该要对应解密第二轮中MixColumns操作的输入,即ShiftRows的输出:
ShiftRows:
49 45 7f 77
db 39 02 de
87 53 d2 96
3b 89 f1 1a
~~
当然,把所有过程展开来看,我们的两份代码对输入明文内容所作操作是完全相同的。区别在于选择的头尾不同,所以对中间的循环体处理自然就不一致了。那么本质上,state经历的每个变换过程是一致的。
2. 等价逆运算
根据前文的描述,虽然加解密过程在结构上大体相似,但实际轮函数变换顺序是不一样的。这就造成了加密和解密需要准备不同的软件、固件模块或是硬件电路,对于同时需要实现加解密的应用而言,这个差异增加了落地成本。为了解决这个问题,AES提供了等价的逆算法。
从Fig 5.和Fig 12.可以看出,标准加解密过程的轮结构分别为:
SubBytes->ShiftRows->Mixcolumns->AddroundKey
invShiftRows->invSubBytes->AddRoundKey->invMixColumns
因此,解密轮的前后两个过程都需要调换。
先来看invShiftRows和invSubBytes,逆行移位和逆字节替代是可以直接交换的,因为行移位改变state中的字节顺序,而字节替代使用S盒替换state中的字节内容。就像先砌墙再刷漆和先刷漆再砌墙一样(当然是在无敌的理想环境),工序的先后不会影响墙壁最终呈现出的色彩和图案。The SubBytes() and ShiftRows() transformations commute. The same is true for their inverses.
AddRoundKey和invMixColumns稍微复杂一些。轮密钥加和逆列混淆都不会改变state中的字节顺序,且它们都是以字为输入单位(computed as a one-dimensional array of word.),每次都对state中的一列进行操作。即两个操作对列的输入是线性相关。如此一来,就可以得到以下等式:
invMixColumns(state ⊕ Roundkey) = invMixColumns(state) ⊕ invMixColumns(Roundkey)
设state第一列为[y0, y1, y2, y3],该轮轮密钥第一列为[k0, k1, k2, k3]。则矩阵表达为:
那么基于这个等式,就可以通过预先对轮密钥生成加入逆列混淆操作,使用转换后的轮密钥代入轮函数运算,从而达到交换AddRoundKey与invMixColumns调用顺序的目的。实际各轮应用如课本图5.10: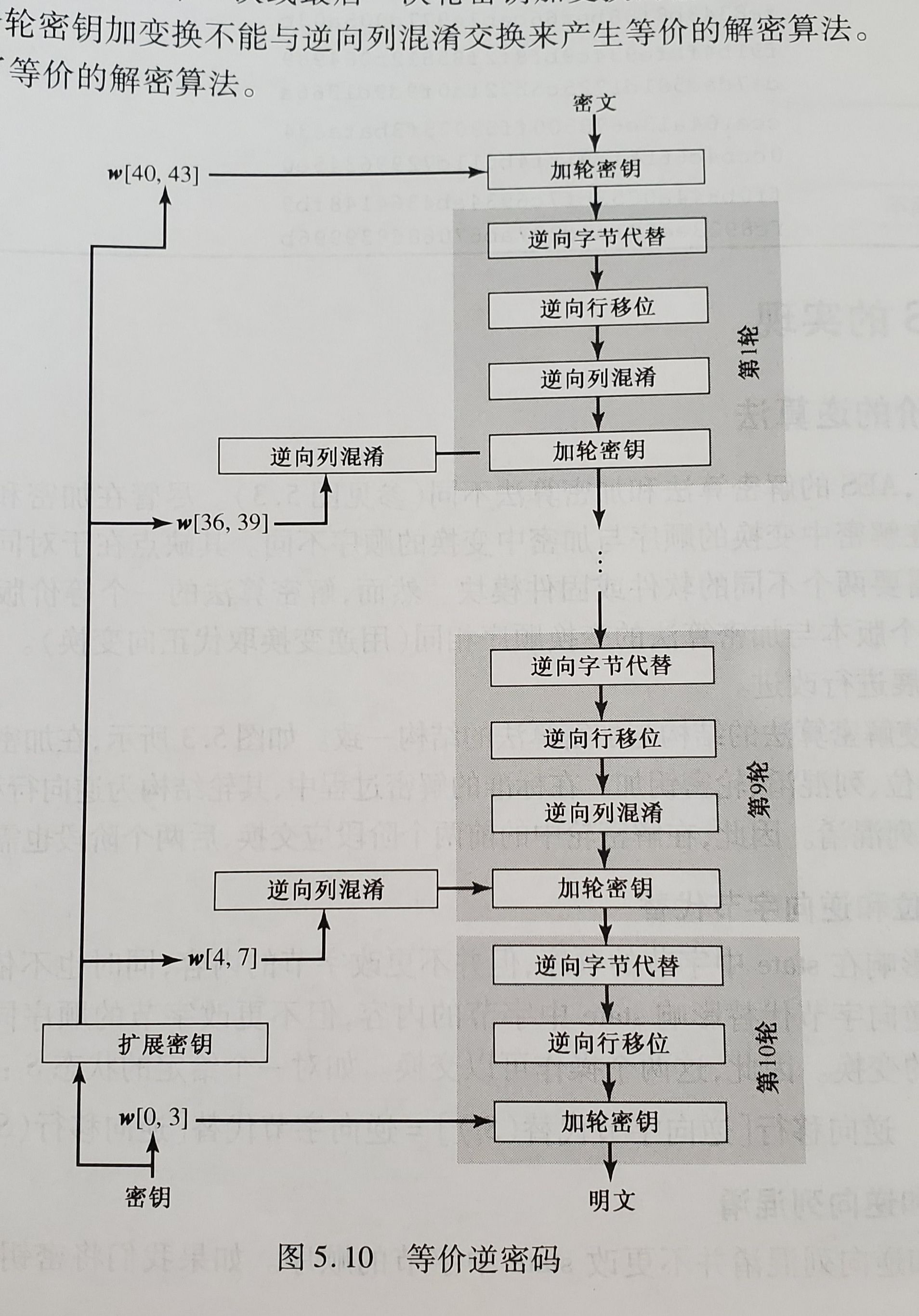
Equivalent Inverse Cipher 实现代码如下1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88/**
* 5.3.5 Equivalent Inverse Cipher
* Fig.15 For the Equivalent function, key expansion should add pre-invMixColumns.
* new para@inv: crypto flag, type-uint8_t, 0-encrypt 1-decrypt
*/
void equ_key_expansion(AES_CYPHER_T mode, uint8_t *key, uint8_t *round, uint8_t inv)
{
uint32_t *w = (uint32_t *)round;
uint32_t t;
int i = 0;
//密钥扩展部分是相同的
printf("Key Expansion:\n");
do {
//KeyExpansion code
} while (++i < g_aes_nb[mode] * (g_aes_rounds[mode] + 1));
//Fig.15 implement equivalent inverse cipher
//此处注意转换数据类型
//invMixColumns传入的是byte 8 bits,而KeyExpansion传入word为32 bits
if (1 == inv)
{
uint8_t *inv_k = (uint8_t *)w;
uint8_t tmp_roundkey[4 * 4 * 15] = {0};
for (i = 1; i < g_aes_rounds[mode]; i++)
{
memcpy(&tmp_roundkey[(i - 1) * 16], &inv_k[i * 16], 16);
inv_mix_columns(mode, &tmp_roundkey[(i - 1) * 16]);
}
//通过w的地址传给round,第一轮和最后一轮的密钥保持不变
memcpy(w + 4, tmp_roundkey, 4 * 4 * (g_aes_rounds[mode] - 1));
}
}
//解密就可以用与加密相同的顺序调用
/**
* section 5.3.5
* Equivalent Inverse Cipher
* switch functions call order to get a efficient struct
*/
int aes_equ_decrypt(AES_CYPHER_T mode, uint8_t *data, uint8_t *key)
{
uint8_t w[4 * 4 * 15] = {0}; /* round key */
uint8_t s[4 * 4] = {0}; /* state */
int nr;
/* key expansion for equ-inverse algorithm*/
equ_key_expansion(mode, key, w, 1);
memcpy(s, data, 4 * g_aes_nb[mode]);
/* start AES cypher loop over all AES rounds */
for (nr = g_aes_rounds[mode]; nr >= 0; nr--)
{
printf(" [Round %d]\n", g_aes_rounds[mode] - nr);
aes_dump("input", s, 4 * g_aes_nb[mode]);
if (nr < g_aes_rounds[mode])
{
inv_sub_bytes(mode, s);
aes_dump("invSubBytes", s, 4 * g_aes_nb[mode]);
inv_shift_rows(mode, s);
aes_dump("invShiftRows", s, 4 * g_aes_nb[mode]);
if (nr > 0)
{
inv_mix_columns(mode, s);
aes_dump("invMixColumns", s, 4 * g_aes_nb[mode]);
}
}
/* do AddRoundKey */
aes_add_round_key(mode, s, w, nr);
aes_dump("RoundKey", &w[nr * 4 * g_aes_nb[mode]], 4 * g_aes_nb[mode]);
aes_dump("state", s, 4 * g_aes_nb[mode]);
}
/* save state (cypher) to user buffer */
memcpy(data, s, 4 * g_aes_nb[mode]);
printf("Output:\n");
aes_dump("plain", data, 4 * g_aes_nb[mode]);
return 0;
}
3. New Flag
接下来应该会开分组密码的工作模式这个坑,如果填完就继续开公钥密码学的坑吧(ˉ﹃ˉ)
VII. 参考文献
- AES标准及Rijndael算法解析
- FIPS-197
- Rijndael_Animation_v4_eng
- 有限域GF(2^8)的四则运算及拉格朗日插值
- AES中S盒的生成原理与变化
- 手动推导计算AES中的s盒的输出
- How are the AES S-Boxes calculated
- polynomial in AES MixColumns
- Figure Guide AES
- The Advanced Encryption Standard: Rijndael
VIII. 附录
APPENDIX A
轮密钥扩展过程。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45Key Expansion:
00: rst: 2b7e1516
01: rst: 28aed2a6
02: rst: abf71588
03: rst: 09cf4f3c
04: rot: cf4f3c09 sub: 8a84eb01 rcon: 01000000 xor: 01eb848b rst: a0fafe17
05: equ: a0fafe17 rst: 88542cb1
06: equ: 88542cb1 rst: 23a33939
07: equ: 23a33939 rst: 2a6c7605
08: rot: 6c76052a sub: 50386be5 rcon: 02000000 xor: e56b3852 rst: f2c295f2
09: equ: f2c295f2 rst: 7a96b943
10: equ: 7a96b943 rst: 5935807a
11: equ: 5935807a rst: 7359f67f
12: rot: 59f67f73 sub: cb42d28f rcon: 04000000 xor: 8fd242cf rst: 3d80477d
13: equ: 3d80477d rst: 4716fe3e
14: equ: 4716fe3e rst: 1e237e44
15: equ: 1e237e44 rst: 6d7a883b
16: rot: 7a883b6d sub: dac4e23c rcon: 08000000 xor: 3ce2c4d2 rst: ef44a541
17: equ: ef44a541 rst: a8525b7f
18: equ: a8525b7f rst: b671253b
19: equ: b671253b rst: db0bad00
20: rot: 0bad00db sub: 2b9563b9 rcon: 10000000 xor: b963953b rst: d4d1c6f8
21: equ: d4d1c6f8 rst: 7c839d87
22: equ: 7c839d87 rst: caf2b8bc
23: equ: caf2b8bc rst: 11f915bc
24: rot: f915bc11 sub: 99596582 rcon: 20000000 xor: 826559b9 rst: 6d88a37a
25: equ: 6d88a37a rst: 110b3efd
26: equ: 110b3efd rst: dbf98641
27: equ: dbf98641 rst: ca0093fd
28: rot: 0093fdca sub: 63dc5474 rcon: 40000000 xor: 7454dc23 rst: 4e54f70e
29: equ: 4e54f70e rst: 5f5fc9f3
30: equ: 5f5fc9f3 rst: 84a64fb2
31: equ: 84a64fb2 rst: 4ea6dc4f
32: rot: a6dc4f4e sub: 2486842f rcon: 80000000 xor: 2f8486a4 rst: ead27321
33: equ: ead27321 rst: b58dbad2
34: equ: b58dbad2 rst: 312bf560
35: equ: 312bf560 rst: 7f8d292f
36: rot: 8d292f7f sub: 5da515d2 rcon: 1b000000 xor: d215a546 rst: ac7766f3
37: equ: ac7766f3 rst: 19fadc21
38: equ: 19fadc21 rst: 28d12941
39: equ: 28d12941 rst: 575c006e
40: rot: 5c006e57 sub: 4a639f5b rcon: 36000000 xor: 5b9f637c rst: d014f9a8
41: equ: d014f9a8 rst: c9ee2589
42: equ: c9ee2589 rst: e13f0cc8
43: equ: e13f0cc8 rst: b6630ca6
APPENDIX B
输出内容根据FIPS-197中Figure 5. Pseudo Code for the Cipher 与Figure 12. Pseudo Code for the Inverse Cipher描述的加解密函数实现得来,展示了经过各变换后内存中state的结果。
1 | 加密 |
1 | 解密 |