分组密码算法工作模式

过去的一年里经历了很多事情，也算尝尽悲欢离合。在我写完高级加密标准-AES之后，计划过半年左右可以把这篇文章完成。但真是没想到高通新方案做下来这么累人，几经波折到现在临近SOP，基础软件平台和操作系统部分基本不太报问题。趁之前出差空闲抽时间把QNX IPC相关的内容做了些demo玩，翻sdk手册看着看着就点到openssl里去了，赶巧顺着把这个摊子收尾。

概述

分组密码是一种加解密方案，它将一个明文分组作为整体加密并且通常得到的是与明文等长的密文分组。一般来说，分组密码的应用范围比流密码要广泛。在接下来的章节里也会提到，使用某些工作模式时，分组密码可以获得与流密码相同的效果。在密码学课堂上，第3章中已经提及分组密码与流密码的概念，在第6章全面地讲解了分组密码的工作模式。

最早的分组密码标准可以追溯到1980年发布的FIPS PUB 81 DES MODES OF OPERATION，网上找到的都是影印版本，果然够古老。在这篇规范中主要定义了DES的分组操作，以64位即8字节对数据块进行处理。到2001年NIST发布了800-38A，相比FIPS 81，800-38A更加广义地描述了分组模式，没有对底层密码算法做限定，基本适用于所有分组密码。

这篇文章主旨是对AES的复习延申，所以在下面章节中分析分组模式的底层密码算法都钦定AES。不同于AES原理部分的学习，分组密码模式几乎没有涉及到多少数学理论知识，简单了很多。在掌握了AES核心部分后，结合分组模式就可以将特定16字节数据的处理扩展为对任意长度数据适用。

五种标准工作模式

达到处理任意长度数据这个目的大致有两种做法，一是通过填充（padding）将输入的原始数据扩展为16的倍数，使其符合AES轮运算要求，如ECB和CBC；另一种则是在分组设计中使用IV（初始化向量）、AES输出或分组结果作为输入进入AES轮运算。而待加密的原始数据留在之后与AES轮运算输出内容做异或操作，如CFB与OFB。在这一章中将会介绍各个模式的特点、适用场景、发生bit错误时影响范围以及明文泄露会带来怎样的风险。

ECB - Electronic Code Book

电码本模式实在是太乃一吾了，几乎没有什么需要解释的地方，直接贴图：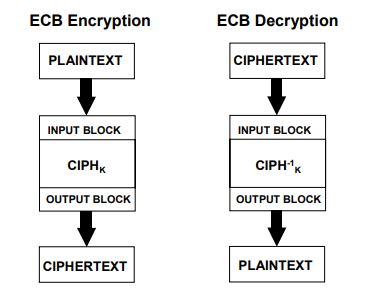
ASE-ECB

可以看到ECB就是多个AES core的组合，一次处理一组明文分块，每次使用相同的密钥，即每组明文都有唯一的密文与之对应。电码本的命名也正是源于这种特征。另外，ECB模式要求待处理的数据长度为16的倍数，当数据长度不满足要求时则先进行填充操作。填充有很多方式，比如ISO 7816-4，这个是智能卡的标准；还有PKCS5，ANSI_X923等等。

电码本模式比较适合处理小数据，如传递加密密钥，或是内部定义的UART或SPI协议数据。对于很长的数据使用ECB模式就可能不安全。尤其在一段消息中存在若干相同的明文组，那么密文也会出现对应数量的相同密文组。

由于ECB模式的分组之间毫无干系，所以在传输过程中发生的bit错误仅仅影响其存在的一个分组。

CBC - Cipher Block Chaining

为了克服ECB的弱点，最简单的应对方法是对明文组做一些预处理，CBC模式在加密运算前将当前明文组与上一组的密文输出做异或运算，如此一来加密算法每次的输入就与明文分组没有固定关系。与ECB模式一样，CBC也要求待处理数据长度为16的倍数。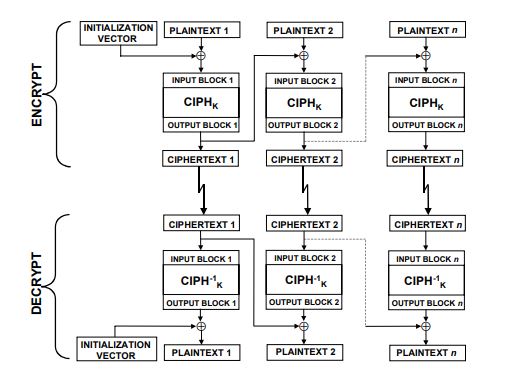
AES-CBC

CBC要求第一个明文块与一个初始化向量（IV）异或后再加密，以产生第一个密文分组。解密时使用第一个解密结果与IV异或恢复出第一个明文块，所以消息收发双方必须要共享IV。另外，由于加密时除第一组以外，之后每一组的输入都需要上一组密文参与，所以CBC模式的加密无法做到并行处理；而解密时已经得到了完整的密文，所以解密运算可以做到并行。

当传输过程中发生bit错误时，错误将会影响本组及下一组共两组明文的解密结果。

CBC在分组密码中应用非常广泛，设计模式也被用于实现消息认证算法（DAA与CMAC）。

简单的CBC模式加解密实现如下：

/**
 * AES Cipher Block Chainning Mode
 */
int aes_encrypt_cbc(AES_CYPHER_T mode, uint8_t *data, int len, uint8_t *key,
                    uint8_t *iv)
{
    int ret = 0;
    uint8_t *d;      //data block
    uint8_t *i;      //input block
    uint8_t *iv_tmp; //iv
    int len_tmp = len;

    int n;           //counter, from 0 to 31
    d = malloc(len);
    memcpy(d, data, len);
    iv_tmp = malloc(len);
    memcpy(iv_tmp, iv, 16);
    i = malloc(len);

    while (len_tmp)
    {
        //iv xor data block
        for (n = 0; n < 16 && n < len_tmp; n++)
        {
            i[n] = d[n] ^ iv_tmp[n];
        }
        //this round's cipher equ next round's iv
        //so prepare it, the n is next round's index
        for (; n < 16; n++)
        {
            i[n] = iv_tmp[n];
        }
        aes_encrypt(mode, i, key);
        iv_tmp = i;
        if (len_tmp <= 16)
        {
            break;
        }
        len_tmp -= 16; //control the loop
        d += 16; //pointer address add
        i += 16; //pointer address add
    }

    memcpy(data, &i[16 - len], len);

    return ret;
}

/**
 * AES Cipher Block Chainning Decrypt
 * decryption can be performed in parallel
 */
int aes_decrypt_cbc(AES_CYPHER_T mode, uint8_t *data, int len, uint8_t *key,
                    uint8_t *iv)
{
    int ret = 0;
    uint8_t *d; // data
    uint8_t *i; // input
    uint8_t *iv_tmp; // iv tmp
    int len_tmp = len;

    d = malloc(len);
    i = malloc(len);
    memcpy(i, data, len);
    iv_tmp = malloc(len);
    memcpy(iv_tmp, iv, 16);
    //这里预先把密文数据放在iv的后面，当然也可以起(len / 16)个线程同时处理
    memcpy(iv_tmp + 16, data, len - 16); // perpare iv

    while (len_tmp)
    {
        aes_equ_decrypt(mode, i, key);
        for (int n = 0; n < 16; n++)
        {
            d[n] = i[n] ^ iv_tmp[n];
        }
        if (len_tmp <= 16)
        {
            break;
        }
        len_tmp -= 16;
        d += 16;
        i += 16;
        iv_tmp += 16;
    }

    memcpy(data, &d[16 - len], len);
    free(&d[16 - len]);

    return ret;
}

CFB - Cipher FeedBack

前两种模式在实际使用过程中大都需要对原始数据进行填充，而这一节中讨论的密文反馈模式则可以通过移位将分组密码模拟成流密码使用。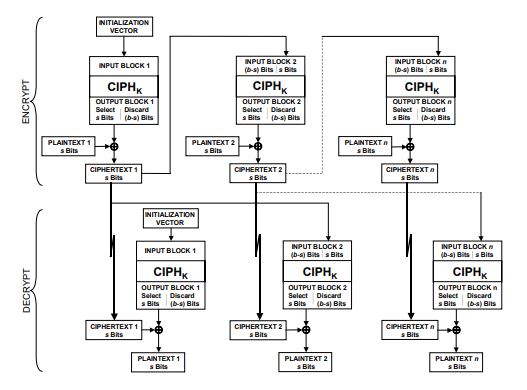
AES-CFB

首先看加密过程，加密函数的输入是128位的移位寄存器，第一组输入为初始向量IV。加密函数输出最左边的s位与明文第一个s位分段内容异或得到第一个密文单元；移位寄存器左移s位，随后将密文单元填入移位寄存器最右边s位产生下一组加密函数的输入数据，直至所有明文单元被加密完。
解密过程同理，但有一个比较容易被忽视的点在于解密过程中使用的也是加密函数而非解密函数。原因很容易解释：将AES的部分看作一个整体，密文通过明文与算法输出异或得到，那么解密时只有将密文与算法输出做异或才能够正确还原出明文。实际上，在CFB, OFB, CTR模式中，解密过程使用的都是加密函数。这也是我在高级加密标准-AES中所提到“不过AES中加密被认为比解密更加重要”的原因之一。

而CFB模式的bit错误影响相对复杂一些，当某次传输中错误存在于s bits中，其造成的影响直到被左移出128位移位寄存器才结束，即bit错误影响范围为1+(b/s)组明文。虽然看起来受影响的组数更多，但由于CFB模式每轮只产生s bits的有效数据，实际上影响的总比特位与CBC是一样的。

我印象中以前上课的时候有同学看到bits移位突然脑子转不过来啊，认为该组解密后错误仅存在于算法输出的s bits中，这里也提一下。因为我们的假设是在密文传输过程中信道存在噪声导致接收到的数据出现比特翻转错误。而AES轮运算中shiftrows与mixcolumns两个过程结合能够将一个bit的错误扩散到整个state上（mixcolumns将错误扩散到一整列，下一轮的shiftrows将一列错误分散到不同列，再由mixcolumns扩散到整个state），导致整组数据报废，不存在某个或某几个位置的字节幸免。
而这又引出一个有意思的话题：针对AES的差分错误分析，以AES-128为例，加解密过程包含10轮运算，但是要注意最后一轮仅仅做了subbytes, shiftrows, addroundkey三个运算，这就导致如果在第9轮的shiftrows之后注入1bit错误，到第10轮结束仅仅会影响到4个字节数据，且发生错误的数据位置与注入错误的列相关，遍历四种错误注入组合后能够推导出末轮的轮密钥，从而反推出AES key。不过这两个点和CFB模式没啥关系，发散了一下(/ω＼)

CFB可以被当作流密码使用，其的密文与明文等长，能够最高效地利用信道传输能力。相比之下分组密码会在解密的最后一轮至多会丢弃127 bits的数据，即最多会浪费127 bits的传输能力。但CFB并不是典型的流密码，它的明文也参与了位流的生成。

NIST中还介绍了cfb1，cfb8和cfb64等模式，一般来说cfb8比较常用。下面是cfb8和cfb128的简单实现：

/**
 * Cipher Feedback Mode
 * 128 bits shift, next round input equ cipher
 * no need padding
 * A.K.A. full-block CFB
 * enc is encrypt flag, 0-decrypt 1-encrypt
 */
int aes_encrypt_cfb128(AES_CYPHER_T mode, uint8_t *data, int len, uint8_t *key,
                       uint8_t *iv, int *num, int enc)
{
    int ret = 0;
    int n, l = 0;
    uint8_t *iv_tmp;
    uint8_t *cipher;

    cipher = malloc(len);
    iv_tmp = malloc(16);
    if (cipher == NULL || iv_tmp == NULL)
    {
        printf("malloc failed\n");
        return -1;
    }
    memcpy(iv_tmp, iv, 16);

    n = *num; // data len check

    while (l < len)
    {
        if (n == 0)
        {
            aes_encrypt(mode, iv_tmp, key);
        }
        if (enc)
        {
            cipher[l] = iv_tmp[n] ^= data[l];
        }
        else
        {
            cipher[l] = iv_tmp[n] ^ data[l];
            iv_tmp[n] = data[l];
        }
        l++;
        n = (n + 1) % 16;
        *num = n;
    }
    memcpy(data, cipher, len);

    return 0;
}

/**
 * cfb 8 bits shift
 * enc: 0-decrypt 1-encrypt
 */
int aes_encrypt_cfb8(AES_CYPHER_T mode, uint8_t *data, int len, uint8_t *key,
                     uint8_t *iv, int enc)
{
    int ret = 0;
    int n, l = 0;
    uint8_t *iv_tmp = malloc(32 + 1);
    memcpy(iv_tmp, iv, 16);
    memcpy(iv_tmp + 16, iv, 16);
    uint8_t *d = malloc(len);

    while (l < len)
    {
        aes_encrypt(mode, iv_tmp, key);
        d[l] = iv_tmp[32] = iv_tmp[0] ^ data[l];
        // printf("%02x\n", d[l]);
        if (0 == enc)
        {
            iv_tmp[32] = data[l];
        }
        //shift 8 bits
        for (int i = 16; i < 32; i++)
        {
            iv_tmp[i] = iv_tmp[i + 1];
        }
        memcpy(iv_tmp, &iv_tmp[16], 16);
        l++;
    }

    memcpy(data, d, len);
    free(iv_tmp);
    free(d);

    return ret;
}

OFB - Output FeekBack

OFB的结构与CFB有些相似，同样可以模拟流密码。但OFB使用加密函数的输出作为下一轮算法输入，所以其加解密过程都不可以并行运算，而CFB的解密过程可以并行。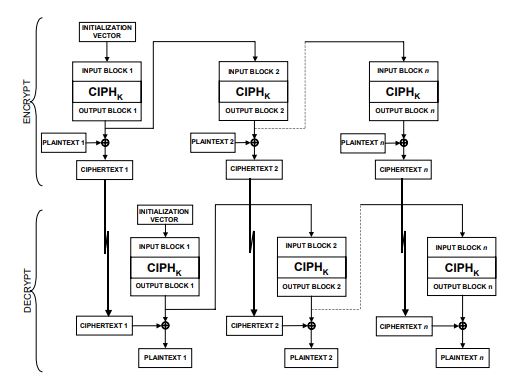
AES-OFB

OFB极其适合在易出现噪音的信道中传输数据，其bit错误不会发生扩散，仅仅影响对应的一个bit位。在传输数字信号，音视频这种单比特错误容忍度较高或者以纠错码编码过的数据简直无敌。但是要注意OFB的iv必需是一个时变值，因为OFB的加密输出完全不依赖明文，仅仅与iv和key相关。假如iv和key都是固定值，等同于与明文进行异或的输出就是固定的，一旦这些输出被攻击者碰撞出来，通过简单的异或操作就能将密文还原成明文。另一个问题是OFB抵抗消息流篡改能力很弱，因为其bit错误不会扩散，那么攻击者完全可以在密文中修改bit值并且更新校验码，从而使改动不被纠错码发现，破坏了信息安全的不可篡改性。

代码简单实现如下：

/**
 * AES OFB
 * do remember this mode requires iv is a nonce.
 */
int aes_encrypt_ofb(AES_CYPHER_T mode, uint8_t *data, int len, uint8_t *key,
                    uint8_t *iv)
{
    int ret, l = 0;
    uint8_t *iv_tmp = malloc(16);
    memcpy(iv_tmp, iv, 16);

    while (l < len)
    {
        aes_encrypt(mode, iv_tmp, key);
        for (int i = 0; i < 16 && l + i < len; i++)
        {
            data[l + i] ^= iv_tmp[i];
        }
        l += 16;
    }

    free(iv_tmp);

    return ret;
}

CTR - Counter

CTR即计数器模式，通篇下来我感觉对这个模式最陌生，翻了翻课本发现真是讲了个寂寞难怪没印象，还是看文献靠谱。从图上可以看到，加解密流程都不算复杂，有一些类似OFB，甚至可以把它叫做IFB（input feedback哈哈）？因为NIST批准的分组模式中，除了ECB之外都需要包含反馈机制，所以可以将counter理解为input block的反馈结果（forward cipher to a set of input blocks, called counters）。

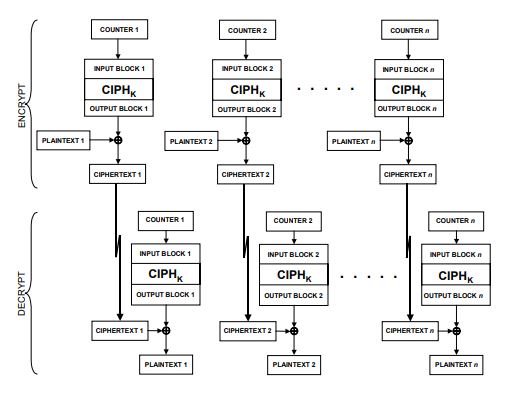
AES-CTR

CTR模式中counter的初始值T₁必须为时变值（nonce），且各个消息分组所使用的counter值T_i必须是不同的，与OFB同样都需要保证参与明文异或的输出值不能重复，否则将无法保证明文分组的保密性。NIST的附录B中重点讨论了CTR模式的counter block生成准则，有以下两点：1. 组成input值的counter需要由递增函数生成以保证每个counter block不会重复；2. 需要选择一个合适的初始值来保证后续参与到消息分组运算的counters（各组input block）都是唯一的。同时，NIST仅仅是建议了一种安全使用CTR模式的方式，并没有规范counters生成的标准算法。其中一种可以表达为8 bytes nonce + 8 bytes counter。

如nonce值为
9e b7 6f ac 45 af 8e 51 30 c8 1c 46 a3 5c e4 11
第一组input组成方式为 nonce|counter
9e b7 6f ac 45 af 8e 51 00 00 00 00 00 00 00 00
接下来则分别是
9e b7 6f ac 45 af 8e 51 00 00 00 00 00 00 00 01
9e b7 6f ac 45 af 8e 51 00 00 00 00 00 00 00 02
9e b7 6f ac 45 af 8e 51 00 00 00 00 00 00 00 03
...
9e b7 6f ac 45 af 8e 51 ff ff ff ff ff ff ff ff

对于一段消息message，counters需要唯一，所以消息的分组个数不能超过2⁶⁴即消息总大小不超过2⁶⁴x16 bytes，这已经是一个很恐怖的数据量了。就算把counter占位减半，使用12字节nonce和4字节counter，能够处理的消息总大小也达到了64G。

简单的代码实现如下，其中ctr128_inc是一个平平无奇的大数自增

/**
 * increment counter to generate input block
 * do notice the total block number N should
 * less then 2^64 in AES, otherwise the uniqueness
 * of counter block will lost.
 */
void ctr128_inc(uint8_t *counter)
{
    uint32_t n = 16, i = 1;

    do {
        --n;
        i += counter[n]; // increase
        counter[n] = (uint8_t)i; // discard carry if 0xff
        i >>= 8; // clear original value but keep the carry
    } while (n);
}

/**
 * AES CTR
 * 
 */
int aes_encrypt_ctr(AES_CYPHER_T mode, uint8_t *data, int len, uint8_t *key,
                    uint8_t *iv)
{
    int ret, l = 0;
    uint8_t *input = malloc(16);
    // the input formated as first 8bytes nonce then fill 8bytes counter
    memset(input, 0, 16);
    memcpy(input, iv, 8);
    uint8_t *counter = malloc(16);
    memcpy(counter, input, 16);

    while(l < len)
    {
        aes_encrypt(mode, input, key);
        for (int i = 0; i < 16 && l + i < len; i++)
        {
            data[l + 1] ^= input[i];
        }
        ctr128_inc(counter);
        memcpy(counter, iv, 8);
        memcpy(input, counter, 16);
        l += 16;
    }

    free(input);
    free(counter);

    return ret;
}

分组模式在图像中的表达

这是我觉得比较有意思的事情，也是想自己实现分组模式的源动力——如何直观地体现AES比特扩散能力以及分组模式对密文混淆程度的影响。至少我非常不认同密码学实验课上用诸如txt，hexview的玩意去看一堆16进制字符串，这些东西在不转化成ascii码之前信息熵就已经高得离谱。使用未经压缩的bitmap位图是不错的选择。在网上草草搜了一圈没看到现成的代码可以抄一抄，直接调openssl接口又感觉太无趣，以前做S.M.A.R.T.的时候玩过一些图像处理，万事俱备刚好从头到尾自己写一遍。
那么这里用的位图是RGB888，不带alpha通道，每个像素占24比特数据。AES中的state包含了五个完整像素点与一个R值。测试用的python代码如下（万年不更新，上古py2.7）：

import sys
from PIL import Image

def openImageFIle(path):
    img = Image.open(path)
    img.show()
    return img

def convertImage2Buf(img, path):
    pixels = img.load()
    f = open(path, "w")
    f.writelines("unsigned char pic[] = {\n")
    for i in range(img.size[0]):
        for j in range(img.size[1]):
            line = ", ".join(map(str, pixels[i, j]))
            line = line + ",\n"
            f.writelines(line)
    f.writelines("};")

def createNewImage(img, path):
    pixels = img.load()
    f = open(path, "r")
    for i in range(img.size[0]):
        for j in range(img.size[1]):
            line = f.readline()
            line = line.strip()
            line = line.split(',')
            line = map(int, line)
            r = line[0]
            g = line[1]
            b = line[2]
            pixels[i, j] = (r, g, b)
    img.show()

# python imgtest.py -in ./pk.bmp ./out.txt
# python imgtest.py -out ./pk.bmp ./test.h
if __name__ == "__main__":
    myimg = openImageFIle(sys.argv[2])
    if sys.argv[1] == "-in":
        createNewImage(myimg, sys.argv[3])
    elif sys.argv[1] == "-out":
        convertImage2Buf(myimg, sys.argv[3])
    else:
        print "param err"

分组模式的差异

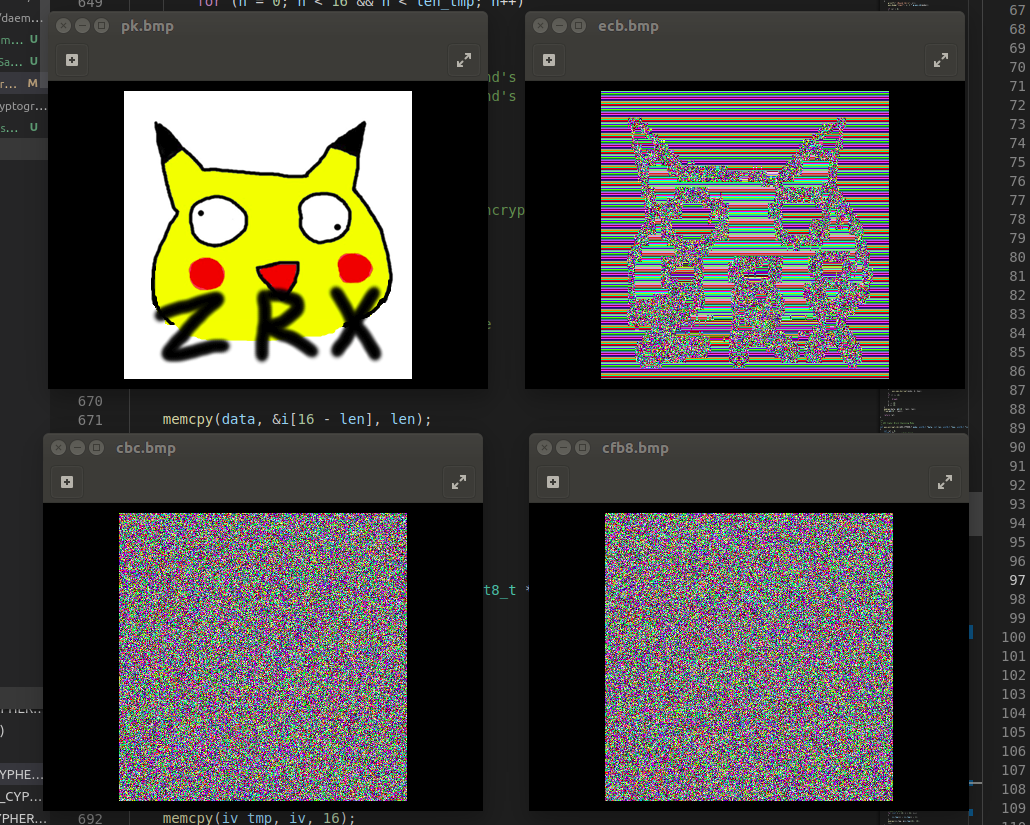
可以看到我的经典互联网冲浪专用头像，经过ECB模式加密后图片轮廓依稀可见，字母几乎可以直接看出来，并且周围的背景色块重复出现，说明原始数据是相同的，如果传递含有语义的数据则难以抵抗统计学分析。很直观地说明了ECB模式无法有效隐藏原始数据中的结构信息。相比之下CBC与CFB则是一片混乱，因为它们在加密过程中每组数据都受到前一组的运算影响，能够将变化扩散到所有分组中。

modes compare

当然也不能放过这张经典的tux比较图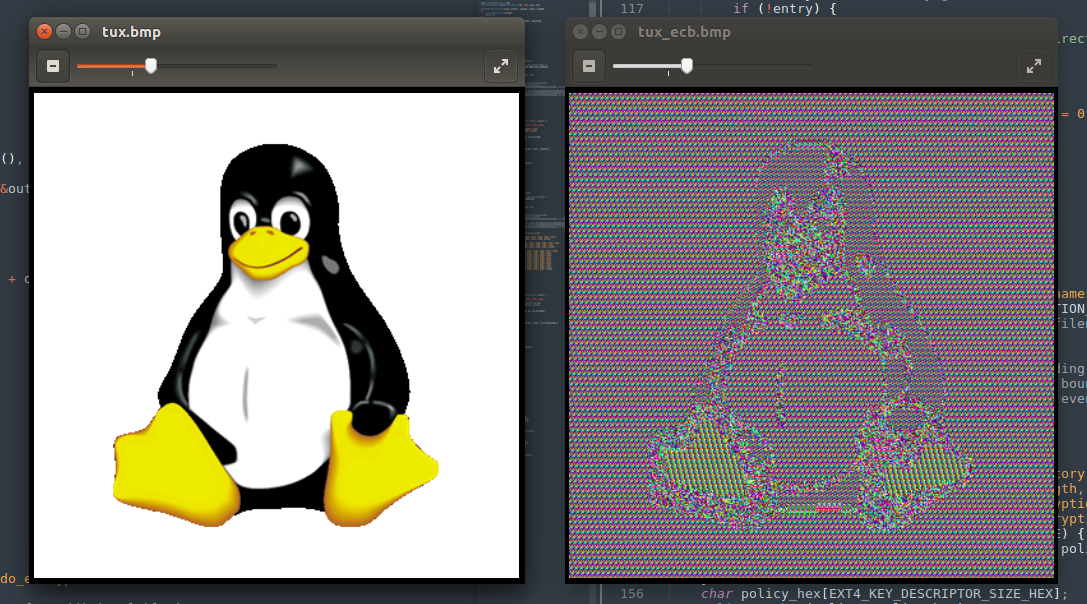
tux

传输中密文的bit错误

传输过程中发生bit错误对解密造成的影响当然也能够通过图像来表达，但实际上效果可能不如想象中那么好。我自己大致尝试了几种模式，如在24位的bitmap中使用CBC模式实验，每个bit会带出6个像素的错误，不过没有体现出对输出bit影响的关系。所以想研究各个模式下的错误扩散直接用hex对比应该会更加合适。
另外在实际应用中，发生错误的场景还包含了加密过程明文错误，传输中的iv或key错误，传输中密文丢失或增加等等情况，密文的bit翻转错误仅仅是其中之一。各分组模式对于以上错误的表现也有所不同。

小结

结合上一篇AES原理介绍，这两篇文章算是把AES基本的理论知识点梳理了一遍。在实际工程应用中还存在着很多新内容和优化项，例如MixColumns可以构建GF(256)上的乘法表来加快加解密速度，如果不打算使用ECB与CBC模式，还能够将这张乘法表缩减一半的内容；还有存储设备上的数据加密会倾向使用XTS模式（如android fbe选择了AES-256-XTS），不需要额外存储iv，加解密都可以并行计算，一个分组损坏不影响后续内容；Android的fde如何处理DEK, KEK，如何应用安全性更强的Scrypt算法以抵抗彩虹表等等。Linux, Andriod系统安全中内核提供的安全加固方案也非常成熟，而掌握对称密码的基本原理，浏览过相关知识发展的过程，再回过头去研究这些内容的设计与实现也会更加得心应手。

new flag

对称密码的复习到这里就告一段落了，接下来将会进入到公钥密码学部分。大致会是数论、Diffie-Hellman、RSA和ECC？不知道什么时候能填完，总之flag先立起来。最后，就以里克尔的诗作为结尾吧：

"Let everything happen to you
Beauty and terror
Just keep going
No feeling is final."

概述