Feistel密码结构

Feistel作为现代密码学中构造分组密码的常用对称结构，我很肯定老师在课上重点分析过。对于这个结构，记忆中一直是模糊的位或、16轮、F函数和纠缠在一起的交叉箭头。想来自己的memory palace也是够奇怪了，居然把feistel和round绑在了一起。直到前段时间无聊搞搞ECU通信加密TEA算法玩，看到图解分析的“1 round”才猛然想起feistel，却又记不起基础理论和实现细节。可能当初手算AES shiftrow mixcolumn留下的心里阴影太大，轰塌了DES大楼，行移位列混淆轮密钥加真^TM琅琅上口。一般教材进入现代密码学首先会介绍分组密码，尤以feistel密码结构为例，进而讲解DES的设计原理。如DES中所做的代换为了使密文唯一而可逆；扩散（P盒）能够弥补古典密码难以抵抗统计分析的弱点；混淆（S盒）则通过打乱密文与密钥的关系来保护密钥。文章中不打算详细分析分组密码，仅对feistel结构及用到相似设计的算法理解做一点记录。

Feistel与分组密码

Feistel密码的命名来自分组密码加密技术的先驱Horst Feistel，这是一条加密方案设计的通用原则，而并非特定的密码方案。一个典型的加解密示意如下图：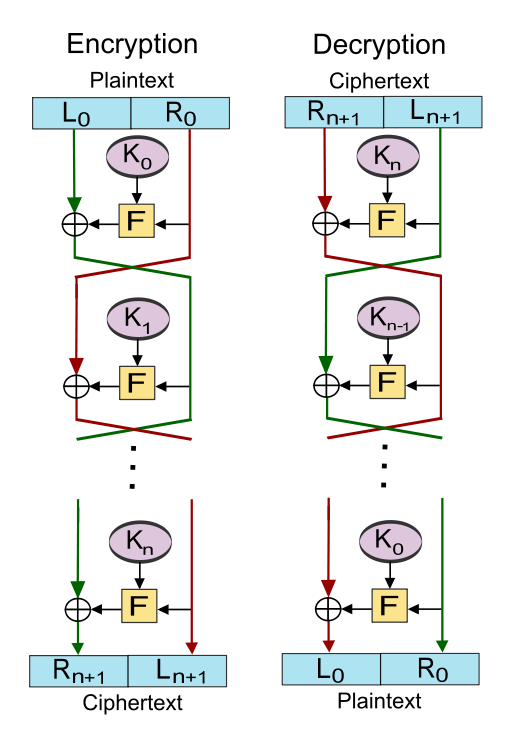
Feistel struct

明文P被分为等长的左右两部分，右半部分R₀与该轮子密钥K经过F函数运算后，再与左半部分L₀做异或运算，最终结果作为下一轮的右半部分输入R₁；同时右半部分R₀直接作为下一轮左半部分输入L₁，这样的一次运算称为一轮。以2 round 1 feistel来描述这个算法，为描述统一增加最后一次左右调换。
加密运算：
L₁ = R₀
R₁ = L₀ ⊕ F(R₀， K₀)
L₂ = R₁ = L₀ ⊕ F(R₀， K₀)
R₂ = L₁ ⊕ F(R₁， K₁) = R₀ ⊕ F(L₀ ⊕ F(R₀， K₀)， K₁)
L₃ = R₂ = R₀ ⊕ F(L₀ ⊕ F(R₀， K₀)， K₁)
R₃ = L₂ = L₀ ⊕ F(R₀， K₀)
解密时子密钥倒序使用：
L₃ = R₂ = L₁ ⊕ F(R₁， K₁) = R₀ ⊕ F(L₀ ⊕ F(R₀， K₀)， K₁)
R₃ = L₂ = R₁ = L₀ ⊕ F(R₀， K₀)
L₂ = R₃
R₂ = L₃ ⊕ F(R₃, K₁) = (R₀ ~~⊕ F(L₀ ⊕ F(R₀， K₀), K₁)) ⊕ F(L₀ ⊕ F(R₀, K₀), K₁)~~ = R₀
L₁ = R₂ = R₀
R₁ = L₂ ⊕ F(R₂, K₀) = (L₀ ~~⊕ F(R₀， K₀)) ⊕ F(R₀, K₀)~~ = L₀
L₀ = R₁
R₀ = L₁

有关feistel的本质理解，cnblogs里看到过这么一段话：

但是对于Feistel结构最本质的特点到底是什么，我也一直不太明白，比较浅显的一点认识就是：每一轮只有一半的比特位参与计算，另外一半直接作为下一轮的输入。

根据算法流程，对于每一轮i迭代输入，左右两边上一轮i-1的输出计算方式如下（以K_i作为第i轮的子密钥）
L_i = R_i-1
R_i = L_i-1 ⊕ F(R_i-1， K_i)
所以严格来说，每轮中左右两半的比特位都参与了运算（异或与F函数），其中一半同时也会直接作为下一轮的输入，但每轮中仅有一半的比特位发生了变化。

Feistel的设计非常精妙，加解密过程使用完全一样的结构，仅初始输入与子密钥调用顺序有区别，所以其加密核心F函数就无需可逆。在软硬件实现上减少了一半的成本。

那么写写代码巩固理论知识

DES加密算法作为使用feistel结构的典型应用，其F函数做了扩展运算、P盒与S盒，完整解析相对复杂。这篇文章主旨还是对feistel的总结，所以选择一个更加轻量、F函数更简单的XTEA算法（TEA升级版本）作为示例来用C实现一遍。但是XTEA在加解密中所用的F函数是不同的，见这篇

关于TEA算法，有种有意思的情况值得引起注意，那就是这个算法不是Feistel密码结构，所以需要分别独立地加密和解密例程。不过，TEA算法在尽可能地接近Feistel密码结构，虽然实际上它并不是--TEA算法使用加法和减法取代了异或运算

XTEA的加密过程如下图所示

XTEA

加解密实现很容易找到源码

// 加密函数
// 输入数据为32x2=64 bits 输入密钥位32x4=128 bits
// 魔术字delta使用黄金比例值的32 bits表示 -> 0.618 * 2^32
void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
    unsigned int i;
    uint32_t v0 = v[0], v1 = v[1], sum = 0, delta = 0x9E3779B9;
    for (i=0; i < num_rounds; i++) {
        // v0 = v0 + F1(v1, Delta', SubkeyA)
        v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
        // 更新Delta
        sum += delta;
        // v1 = v1 + F1(v0, Delta", SubkeyB)
        // Delta"仅表示与v0计算中Delta'不同
        v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
    }
    // 更新数组
    v[0] = v0; v[1] = v1;
}

// 解密函数
// 输入数据长度与加密相同
// 解密过程为实现加密过程的反函数 即F2 = F1^-1
void decipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
    unsigned int i;
    // 初始赋值 sum需要取加密过程的最终值
    uint32_t v0 = v[0], v1 = v[1], delta = 0x9E3779B9, sum = delta * num_rounds;
    while(sum) {
        // v1 = v1 - F2(v0, Delta', SubkeyB)
        v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
        // 更新Delta
        sum -= delta;
        // v0 = v0 - F2(v1, Delta", SubkeyA)
        v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
    }
    v[0] = v0; v[1] = v1;
}

写一个main函数验证

// 密钥和数据都定义为32位无符号整型
int main()
{
    uint32_t key[] = {0x0055, 0x0006, 0x4569, 0x9994};
    //uint32_t data[2] = {0x6666, 0x7777};
    uint32_t data[2] = {6, 7};
    unsigned int round = 32;
    printf("加密前原始数据：%u %u\n", data[0], data[1]);
    printf("HEX format：0x%04x 0x%04x\n", data[0], data[1]);
    encipher(round, data, key);
    printf("加密后的数据：%u %u\n", data[0], data[1]);
    printf("HEX format：0x%04x 0x%04x\n", data[0], data[1]);
    decipher(round, data, key);
    printf("解密后的数据：%u %u\n", data[0], data[1]);
    printf("HEX format：0x%04x 0x%04x\n", data[0], data[1]);
    return 0;
}

输出结果

加密前原始数据：6 7
HEX format：0x0006 0x0007
加密后的数据：4284586257 1255763364
HEX format：0xff619911 0x4ad96da4
解密后的数据：6 7
HEX format：0x0006 0x0007

加密前原始数据：26214 30583
HEX format：0x6666 0x7777
加密后的数据：746062399 1429439190
HEX format：0x2c78023f 0x553382d6
解密后的数据：26214 30583
HEX format：0x6666 0x7777

实际上，这个main函数并不是通用使用方式，而是按照XTEA要求的64 bits数据与128 bits密钥构造输入值去做验证。通用的方法，如一个字符串，可以参考udaykanthr的github
主要对不同长度下剩余不足64 bits情况的数据分别填充处理。

密码学不要自己造轮子

Feistel在很多经典的密码算法中都有用到。要明确，feistel是一类密码结构，并不是某种特定的密码算法。实际上，对于feistel结构而言，不同的F函数就意味着不同的密码算法。我来写一个很弱鸡的F函数充当反面教材。

做8轮计算，最后把左右输出交换。加解密时调用函数是相同的，但各轮中输入的密钥需要倒序。

laji_feistel

#include <stdint.h>
#include <stdio.h>

/* take 64 bits of data in v[0] and v[1] and 128 bits of key[0] - key[3] */
void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4])
{
    unsigned int i;
    uint32_t L = v[0], R = v[1], tmp = 0;
    printf("origin v0 is %d, v1 is %d\n", L, R);
    for (i = 0; i < num_rounds; i++)
    {
        tmp = R;
        R = (((R >> 4) + key[i] << 5) ^ L);
        L = tmp;
        printf("v0 is %d, v1 is %d\n", L, R);
    }
    v[0] = R; v[1] = L;
}

int main()
{
    uint32_t key[]   = {0x0055, 0x0006, 0x4569, 0x9994, 0x1234, 0x0325, 0x1206, 0x0227};
    uint32_t key1[]  = {0x0227, 0x1206, 0x0325, 0x1234, 0x9994, 0x4569, 0x0006, 0x0055};
    uint32_t data[2] = {0x6666, 0x7777};
    //uint32_t data[2] = {6, 7};
    unsigned int round = 8;
    printf("加密前原始数据：%u %u\n", data[0], data[1]);
    printf("HEX format：0x%04x 0x%04x\n", data[0], data[1]);
    encipher(round, data, key);
    printf("加密后的数据：%u %u\n", data[0], data[1]);
    printf("HEX format：0x%04x 0x%04x\n", data[0], data[1]);
    encipher(round, data, key1);
    printf("解密后的数据：%u %u\n", data[0], data[1]);
    printf("HEX format：0x%04x 0x%04x\n", data[0], data[1]);
    return 0;
}

输出结果

加密前原始数据：26214 30583
HEX format：0x6666 0x7777
origin v0 is 26214, v1 is 30583
v0 is 30583, v1 is 40934
v0 is 40934, v1 is 79863
v0 is 79863, v1 is 754406
v0 is 754406, v1 is 2822071
v0 is 2822071, v1 is 5498630
v0 is 5498630, v1 is 8600855
v0 is 8600855, v1 is 22765030
v0 is 22765030, v1 is 36978103
加密后的数据：36978103 22765030
HEX format：0x2343db7 0x15b5de6
origin v0 is 36978103, v1 is 22765030
v0 is 22765030, v1 is 8600855
v0 is 8600855, v1 is 5498630
v0 is 5498630, v1 is 2822071
v0 is 2822071, v1 is 754406
v0 is 754406, v1 is 79863
v0 is 79863, v1 is 40934
v0 is 40934, v1 is 30583
v0 is 30583, v1 is 26214
解密后的数据：26214 30583
HEX format：0x6666 0x7777

参考

密码算法详解——DES
TEA算法
 记一次iOS使用XTEA微型加密算法
 TEA、XTEA、XXTEA加密解密算法
 udaykanthr/XTEA